NeurIPS2020

Structural Abstraction in RL

Papers

---

Learning Graph Structure with FSA Layer

Daniel D. Johnson, Hugo Larochelle, Daniel Tarlow

Motivation; Deciding connections in graphs is an important part of relational representations ****

Summary: A Layer which suggests extra edges to add to a graph to improve performance on downstream tasks

$L$-Paths

In graph $G = ( N, E )$ , let $L$ be a formal language over $\sum = N \cup E$ $( L \subseteq \sum^*)$

An $L$-Path exists between $n_0$ and $n_t$ if the word corresponding to the $n_0$ to $n_1$ path is in $L$

Regular languages $L$ can be constructed to correspond to specific relations

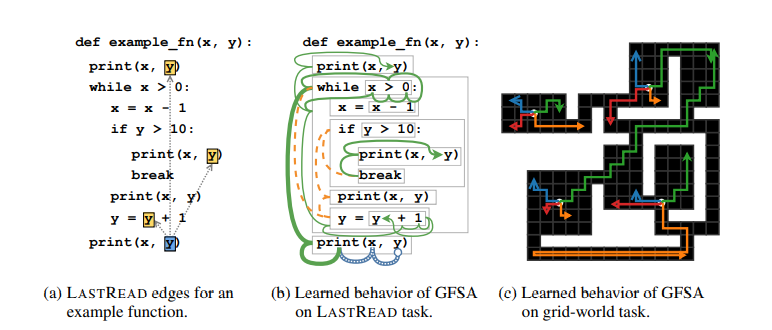
• LastRead
• LastWrite
• NextControlFlow

More generally, the existence of L-paths summarizes the presence of longer chains of relationships with a single pairwise relation. We may not always know which language L would be useful for a task of interest; our approach makes it possible to jointly learn L and use the L-paths as an abstraction for the downstream task.

Graphs as Rewardless POMDPS

• Observations consists of information local to node that agent is at ($\omega_{t+1} \in \Omega_{\tau(n_t+1)}$)
• Action space -

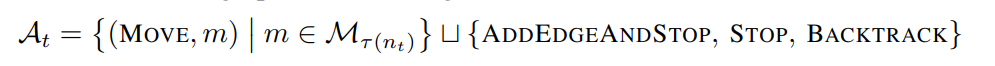
Method

• The agent is parameterised as learnable FSA, to bias it towards adding edges corresponding towards $L$-paths
• Monte carlo estimate for adjacency matrix is computed by collecting trajectories from agent which summarizes the paths that the agent tends to accept.
• Adjacency matrix is computed as -

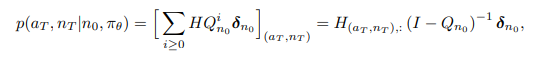
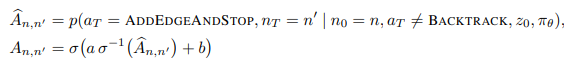
• Adjacency matrix can be viewed as a new weighted edge type. Since it is differentiable with respect to the policy parameters, this adjacency matrix can either be supervised directly or passed to a downstream graph model and trained end-to-end

Experiments

---

Background for Long Horizon Tasks

• In shooting methods such as MPC, a model (learned or known) is used to search for paths
• Sequential methods can suffer from accumulation of error
• Deep RL and shooting methods do not scale well to long horizon tasks

---

Long Horizon Visual Planning with Goal Conditioned Hierarchical Predictors

Karl Pertsch, Oleh Rybkin, Frederik Ebert, Shenghao Zhou, Dinesh Jayaraman, Chelsea Finn, Sergey Levine

Motivation: Current methods don't scale well to long horizon planning. Many sequential planners suffer from accumulation of error.

Background:

• Video interpolation
• Visual planning
• Hierarchical planning

Summary: Use a hierarchical goal conditioned approach to sample trajectories that will

Method:

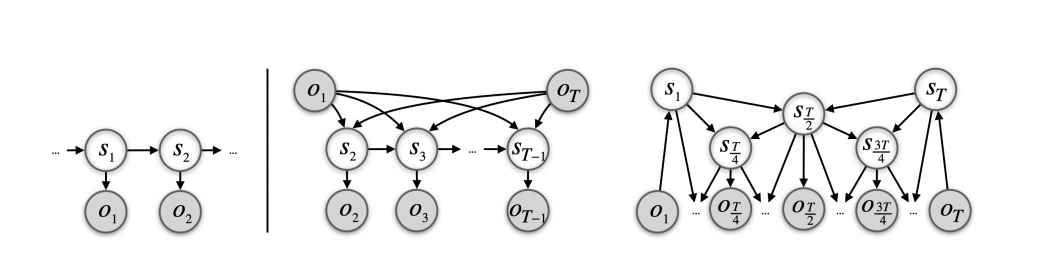
• Train hierarchical predictor $p(s_t | parents(t))$ to predict an intermediate state given start and end states. Recursively use this to plan a path
• Combination of a variational autoencoder and LSTM with latent state composed of deterministic recurrent hidden state and stochastic per time-step latent variable

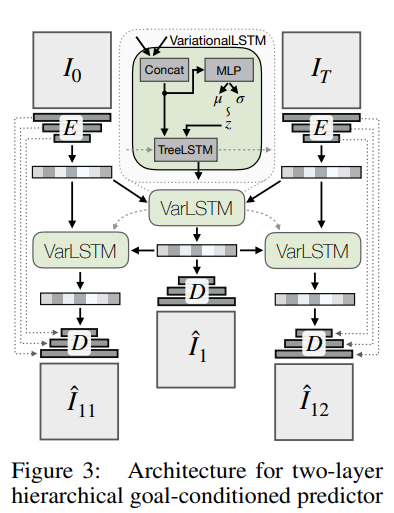
• Instead of optimising for a complete trajectory →
  1. Train neural network to predict expected cost between two states
  2. Sample multiple subgoals
  3. Choose the one with the minimum cost to start and end goals according to cost network

Experiments:

• Video interpolation -

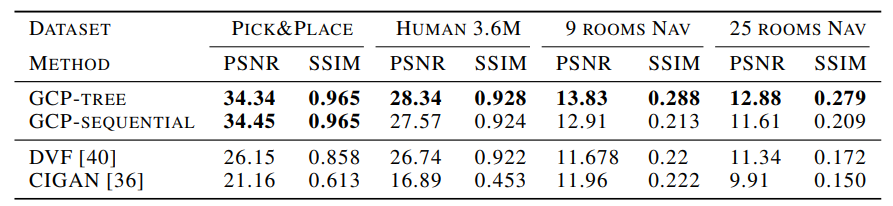
• Visual planning and control -

---

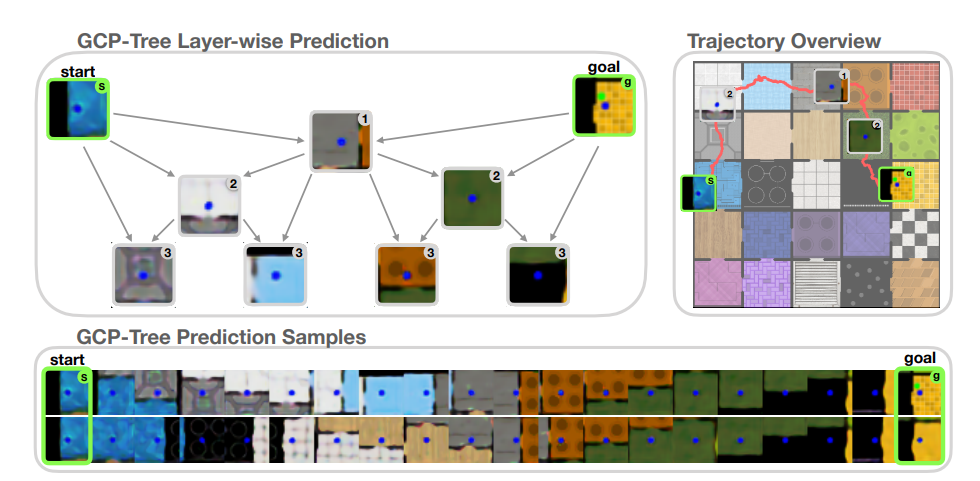
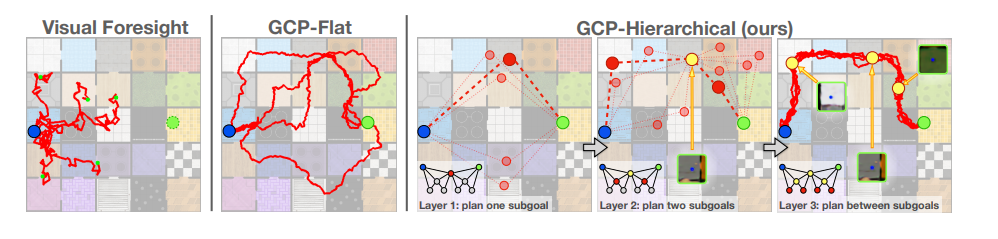
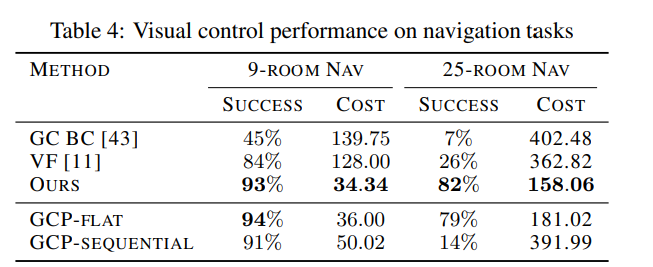
Sparse Graphical Memory for Robust Planning

Scott Emmons, Ajay Jain, Misha Laskin, Thanard Kurutach, Pieter Abbeel, Deepak Pathak

Motivation: Current Deep RL methods don't scale to long-horizon tasks unlike classical methods such as A* search.

Background

• Current graphical memory doesn't scale well to complex environments (both computationally and in terms of error accumulation) or use human intervention to generate the graph

Summary: Combine long horizon ability of classical planning with the flexibility of Deep RL by incorporating graph-based component which is actively kept sparse during exploration.

Method

High level policy - Djikstra's algorithm

Low level policy - D3PG

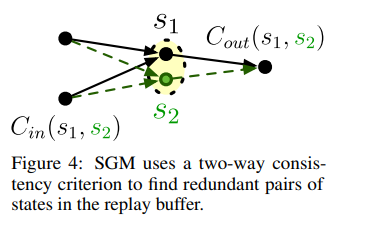
Sparse Graphical Memory is constructed from a buffer of exploration trajectories by retaining the minimal set of states that fail our two-way consistency aggregation criterion

• Two Way Consistency Criterion: Two states are equivalent if they are interchangeable as both goals and starting states.

  (This guarantees that plans in sparsified graph are near optimal in the original graph)

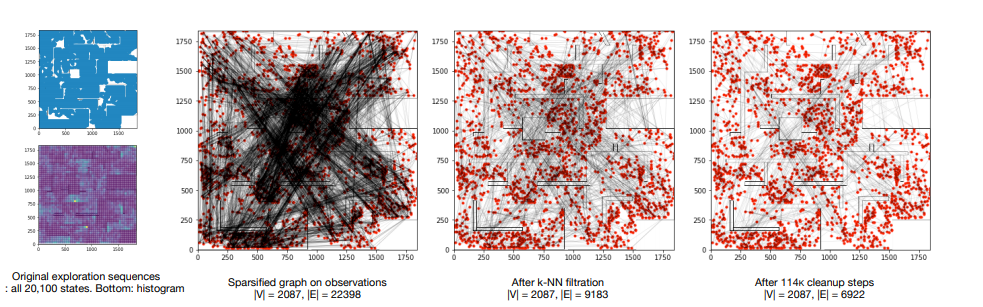
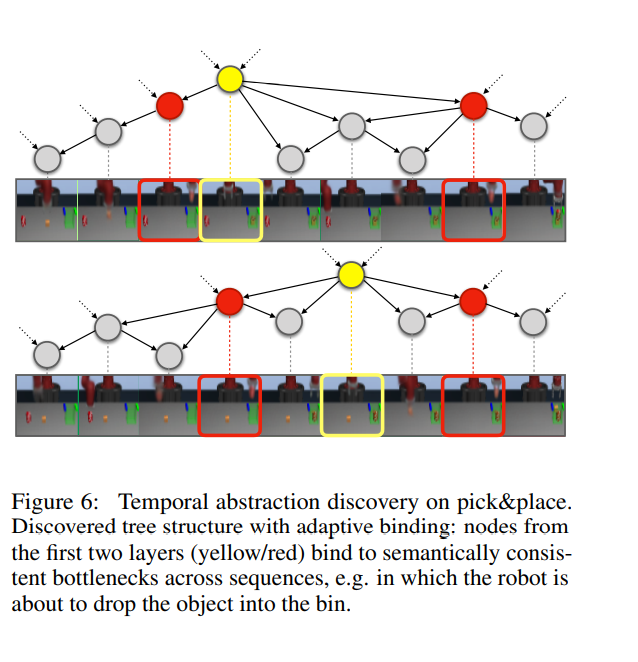
• Cleaning graph -
  1. limit edges for each node to only $k$ of its nearest neighbors
  2. Sample random goal and if the agent cannot traverse between some waypoints $w_i$ and $w_{i+1}$ , then remove that edge

Experiments

---

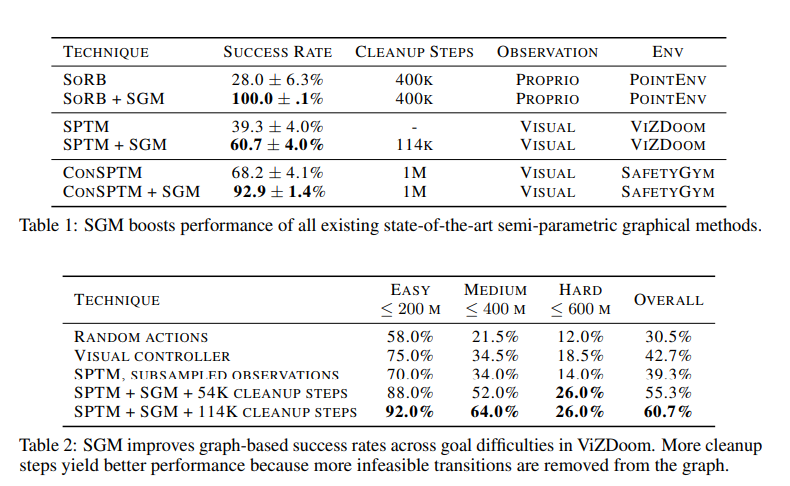
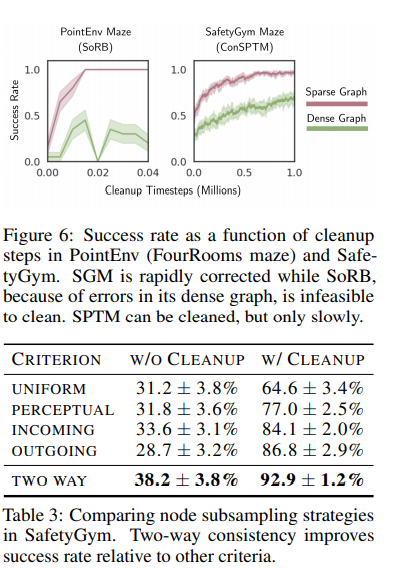
Neurosymbolic RL with Formally Verified Exploration

Greg Anderson, Abhinav Verma, Isil Dillig, Swarat Chaudhuri

Motivation: Safe RL where agent follows some contraints

Background

• Constrained Policy Optimisation
• Shielding
• Formal Verification of Neural Networks

Summary: Uses neurosymbolic policy which can be updated through gradient descent and can be easily verified

Problem Formulation

• Augumented MDP: $M = (S, A, P, \gamma, c, p_0, P^{#}, S_U )$
  • $S$: State Space
  • $A$ : Action Space
  • $P$: Transition Function
  • $\gamma$: Discount Factor
  • $c$: Cost / Reward Function
  • $p_0$: Probability distribution over initial states
  • $P^{#}: S \times X \rightarrow 2^S$ : Defines worst-case bounds
  • $S_U$: Unsafe states
• Policy $\pi$ is safe if all the states reachable with that policy are safe
• Need to find policy $\pi$ that is optimal wr.r.t $J(\pi) = E[\sum_i \gamma^i c_i]$ and safe

Policy Structure

Policy $\pi = (g, \phi, f)$ where action is selected according to

$h(s) = \textbf{if} \ (P^{#}(s, f(s)) ⊆ \phi) \ \textbf{then} \ f(s) \ \textbf{else} \ g(s)$

• $f$ is neural network policy
• $\phi$ is the set of safe states
• $g$ is shield (defined as piecewise linear policies) -

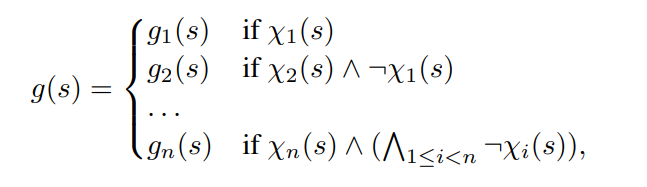
Learning Algorithm

• LIFT: Train a neural network $f$ to imitate $g$
• UPDATE: Update $f$ with policy gradient $\eta \nabla_F J(h)$ to $f'$
• PROJECT: Find improved $g'$ that minimises $D(g', (g, \phi, f'))$ for some Bregman divergence $D$. This is done in a loop where the current policy g is refined further and sub-parts of the policy are optimised with constraints to minimise $D$.

Note: The combined policy stays safe throughout the procedure

Regret Bound

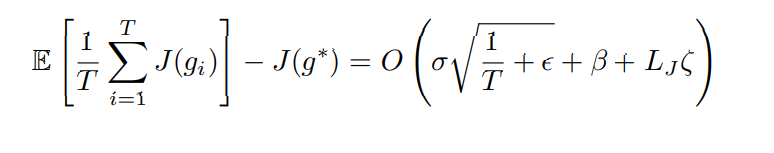
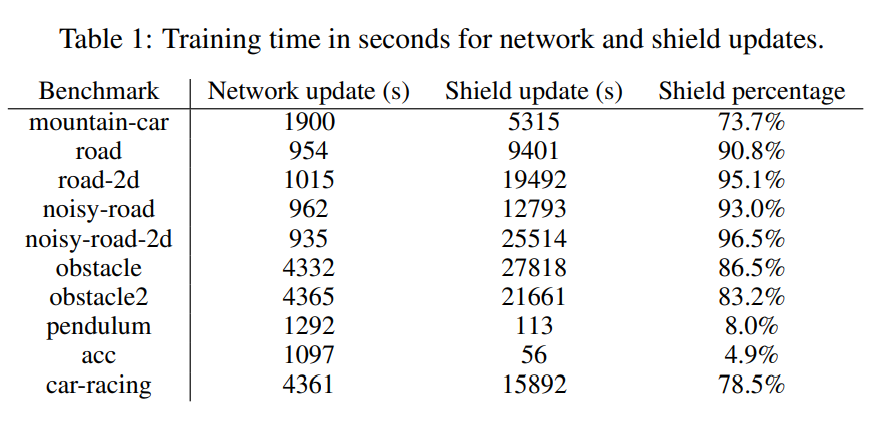
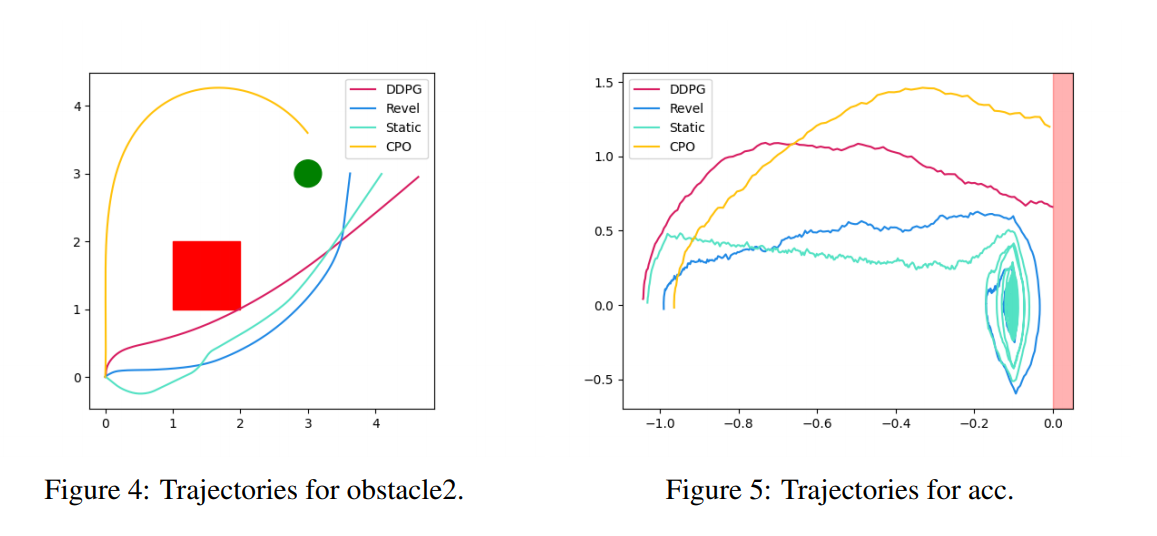
Experiments

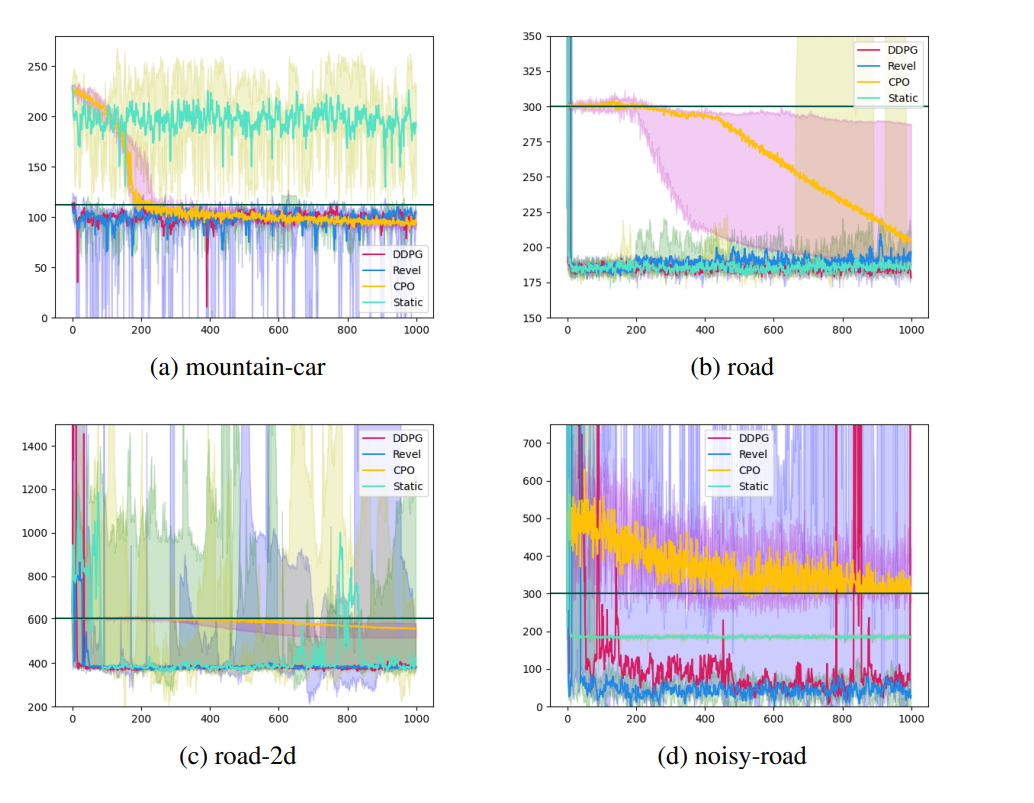
Cost vs episode plots

---

Boolean Task Algebra for Reinforcement Learning

Geraud Nangue Tasse, Steven James, Benjamin Rosman

Motivation: Be able to compose previously learned skills to solve novel tasks

Background:

• Logical compositions as union and intersection of sets of tasks

Summary: Theory devloping boolean algebra for MDPs under some restrictions

Theory

• Prelimianries:

  • Tasks are modelled as MDPs.
  • Collection of tasks is considered to share action space, observation space, transition dynamics and non terminal reward. Terminal reward indicates the task to be completed in specific MDP
  • Reward at terminal state should only take two values

• Boolean Algebra for Tasks

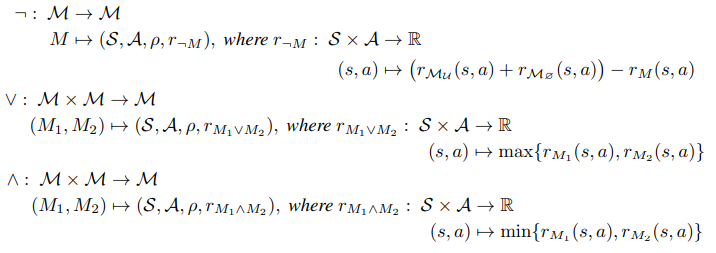
• Extended Reward and Value Functions

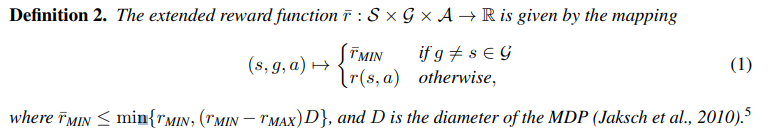
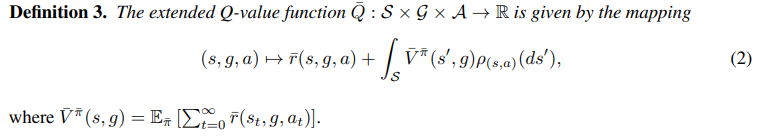
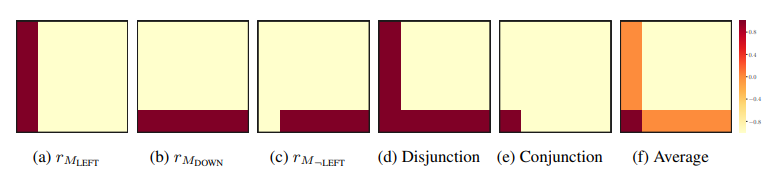
• Boolean Algebra for Value Functions

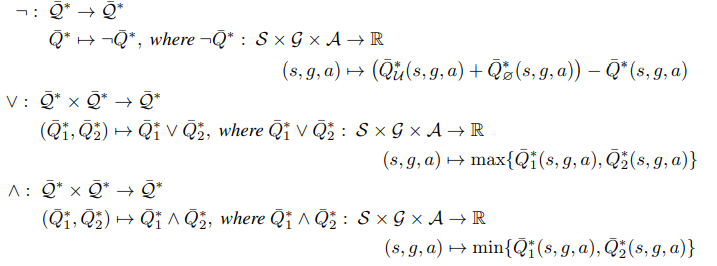
• Homomorphisms between tasks and value functions

Experiments:

• 4 Rooms Environment -

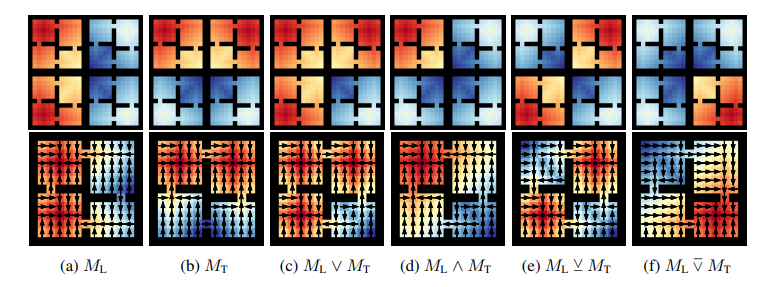
• Find and pick up RGB Ennvironment -

---

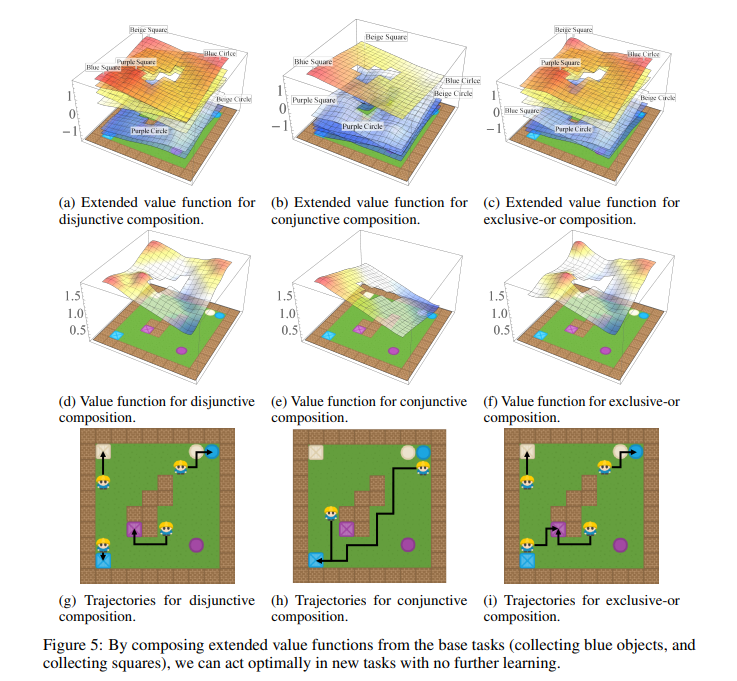
Discussion

• Temporal / spatial / semantic abstraction being achieved through

  1. Memory (graphical / automaton)
  2. Hierarchy
  3. Composition
  4. Translation

• Explanabile and Safe RL requires some sort of abstaction which can be interpreted

• Way forward for RL - similar to language models or through more integration with abstraction methods?